Učivo

Obvody a obsahy (9. třída ZŠ)

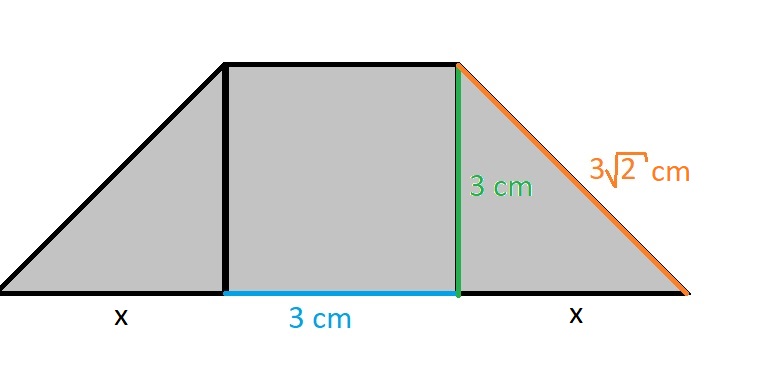
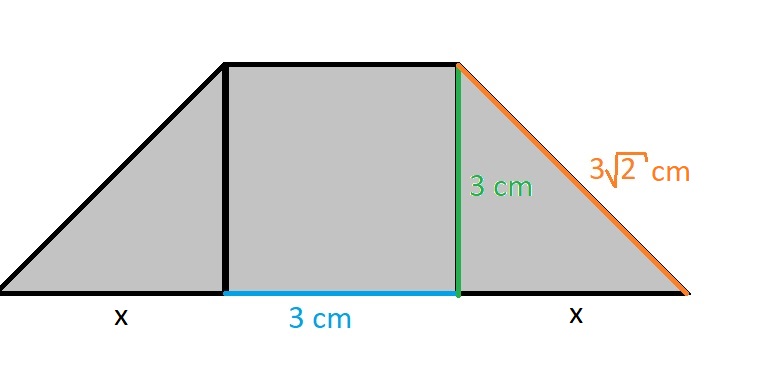
Obsah lichoběžníku vypočítáme pomocí vzorce: $\large S=\frac{(a+c)\cdot v}{2}$ .

Pomocí Pythagorovy věty určíme délku úseku x:
$\large a^{2}=c^{2}-b^{2}$
$\large x^{2}=(3\sqrt{2})^{2}-3^{2}$
$\large x^{2}=9\cdot 2-9=18-9$
$\large x=\sqrt{9}=3 \, \textup{cm}$ .

Délka strany a je tedy:
$\large a=x+3+x$
$\large a=3+3+3=9\, \textup{cm}$ .

Délku stany c a výšku v určíme z obrázku:
$\large c=3 \, \textup {cm}$
$\large v=3 \, \textup {cm}$

Dopočítáme obsah lichoběžníku:
$\large S=\frac{(a+c)\cdot v}{2}$

$\large S=\frac{(9+3)\cdot 3}{2}$

$\large S=\frac{12\cdot 3}{2}=18\, \textup{cm}^{2}$

Obsah lichoběžníku je 18 cm².

14 / 14

Jaký je obsah lichoběžníku?