Učivo

Obvody a obsahy (9. třída ZŠ)

Pro obvod lichoběžníku platí vztah: $\large O=a+b+c+d$ .

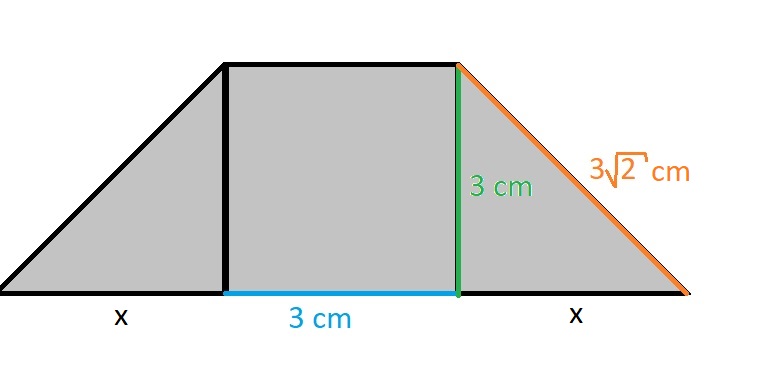
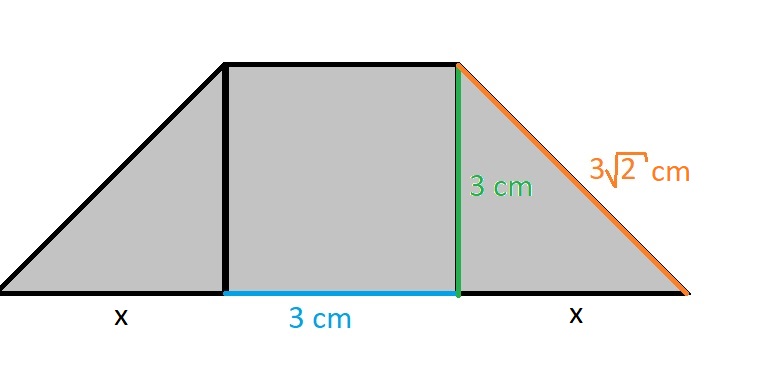
Z obrázku určíme délku jednotlivých stran:
$\large a=x+3+x$
$\large b=3 \sqrt{2}\, \textup{cm}$
$\large c=3 \, \textup {cm}$
$\large d=3 \sqrt{2}\, \textup{cm}$ .

Pomocí Pythagorovy věty určíme délku úseku x:
$\large a^{2}=c^{2}-b^{2}$
$\large x^{2}=(3\sqrt{2})^{2}-3^{2}$
$\large x^{2}=9\cdot 2-9=18-9$
$\large x=\sqrt{9}=3 \, \textup{cm}$ .

Délka strany a je tedy:
$\large a=x+3+x$
$\large a=3+3+3=9\, \textup{cm}$ .

Dopočítáme obvod lichoběžníku:
$\large O=a+b+c+d$
$\large O=9+3 \sqrt{2}+3+3 \sqrt{2}$
$\large O=12+ 6\sqrt{2}$
$\large O=6(2+ \sqrt{2})\, \textup{cm}$
$\large O\doteq 20,5\, \textup{cm}$

Obvod lichoběžníku je $\large \small O=6(2+ \sqrt{2})\, \textup{cm}$ .

13 / 14

Jaký je obvod lichoběžníku?