Učivo

Obvody a obsahy (9. třída ZŠ)

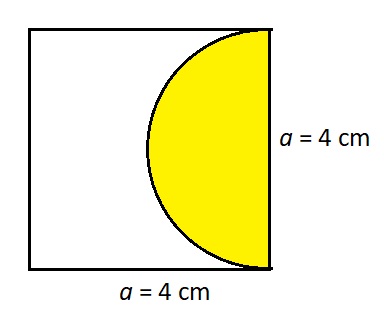
Potřebujeme vypočítat obsah půlkruhu.

Pro výpočet obsahu kruhu platí vztah: S = πr^2. Půlkruh bude mít obsah poloviční: $S _{p}= \frac{\pi \cdot r^{2}}{2}$ .

Na obrázku vidíme délku strany $a=4 \, \textup{cm}$ . Délka strany a odpovídá průměru kruhu d. Poloměr kruhu odpovídá polovině poloměru r. Poloměr kruhu má tedy délku: $r=\frac{a}{2}=\frac{d}{2}=\frac{4}{2}=2\, \textup{cm}$ .

Dosadíme do vzorce a dopočítáme obsah půlkruhu:
$S_{p} = \frac{\pi \cdot r^{2}}{2}= \frac{\pi \cdot 2^{2}}{2}= \frac{\pi \cdot4}{2}$

$S_{p}=\pi\cdot 2=3,14\cdot 2=6,28$
$S_{p}\doteq 6,3$ .

Obsah žluté plochy je 6,3 cm².

6 / 14

Jaký je obsah žluté plochy?