Učivo

Obvody a obsahy (9. třída ZŠ)

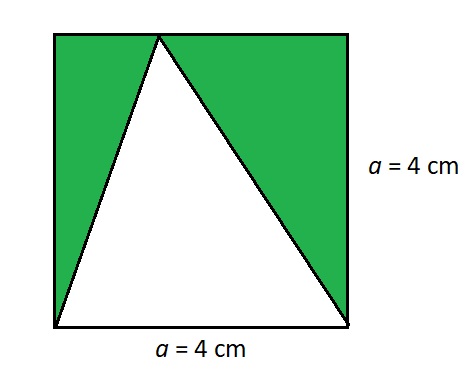
Potřebujeme vypočítat obsah čtverce, poté obsah bílého trojúhelníku. Když odečteme obsah trojúhelníku od obsahu čtverce, tak dostaneme obsah zelené plochy.

Pro výpočet obsahu čtverce platí vztah: $S_{c}=a^{2}$ .

Pro výpočet obsahu trojúhelníku platí vztah: $S_{t} = \frac{a\cdot v_{a}}{2}$ .

Na obrázku vidíme, že délka strany $a=4 \, \textup{cm}$ . Délka výšky je v tomto případě stejná jako délka strany a. Tedy platí: $v_{a}=4 \,\textup{cm}$ .

Dosadíme číselně do vzorců a dopočítáme.

Obsah čtverce:
$S_{c}=a^{2}=4^{2}=16\, \textup{cm}^{2}$ .

Obsahu trojúhelníku:
$S _{t}= \frac{a\cdot v_{a}}{2}=\frac{4\cdot 4}{2}=\frac{16}{2}$ .
$S_{t}=8 \, \textup{cm}^{2}$ .

Obsah zelené plochy:
$S=S_{c}-S_{t}$
$S=16-8=8\, \textup{cm}^{2}$ .

Obsah zelené plochy je 8 cm².

5 / 14

Jaký je obsah zelené plochy?