Lineární funkce 2

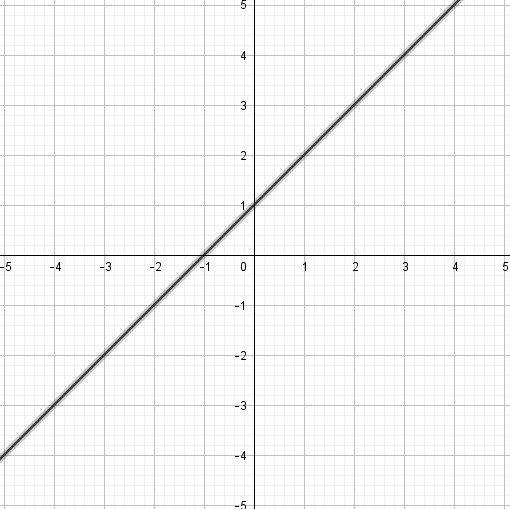
Postupně se dostaneme ke složitějším funkcím. Začneme s posunutím.
Co je důležité?
Nejdřív se podíváme jestli jde o tvar f: y = x nebo f: y = -x. Z obrázku můžeme vidět, že funkce podél osy x roste, takže je rostoucí a má tvar f: y = x.
Z počátku po ose y byla posunuta o +1.
Výsledný tvar tedy je: f: y = x + 1

Z předchozí kapitoly:
Víme, že lineární funkce má předpis: f: y = kx + q a zaznamenává rovnoměrný růst nebo pokles (nebo konstantnost).
Za "základní" můžeme považovat f: y = x (rostoucí) a f: y = -x (klesající).
Pro rostoucí funkci platí, že k >0. Pro klesající funkci platí, že k

3 / 10

Urči předpis funkce: