Lineární funkce 1

Další užitečná věc pro lineární (a další) funkce je umět zjistit průsečíky s osami x a y.
Pokud si představíme kartézskou soustavu souřadnic, kde je dána jakákoliv přímka: například: f: y = -x + 2

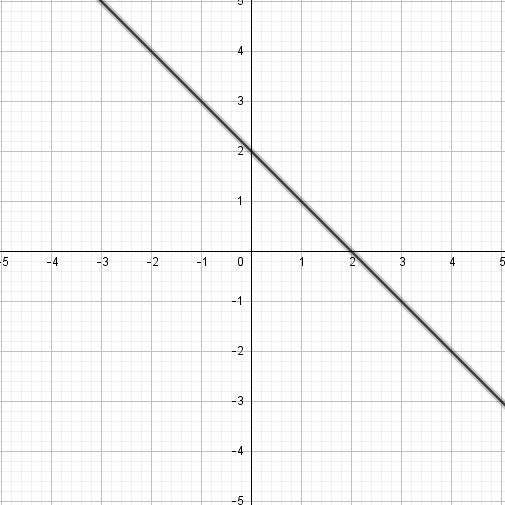
V jakém bodě protíná přímka osu x? V bodě, kde
y-ová souřadnice je nulová. A pro y = 0 dokážeme dopočítat x. Výsledkem je hledaný průsečík s osou x, který značíme: $P_{x} = [x, 0]$ .
Stejně tak průsečík s osou y: x - ová souřadnice je nulová a průsečík značíme: $P_{y} = [0, y]$
Příklad: Vypočti průsečíky s osami x a y funkce
f: y = 3x + 2
1) $P_{x} = [x, 0]$ :
$\\y = 3x + 2\\ 0 = 3x + 2\\ -2 = 3x\\ x = \frac{-2}{3} \\ P_{x} = [ \frac{-2}{3}, 0]$
2) $P_{y} = [0, y]$ :
$\\ y = 3x + 2\\ y = 3 \cdot 0 + 2 \\ y = 2 \\ P_{y} = [0, 2]$

7 / 10

Doplň

Průsečík s osou y funkce f: y = 10x + 1 je roven: . Průsečík s osou y funkce f: y = -3x - 1 je roven: . Průsečík s osou x funkce f: y = -4x + 1 je roven: .

Průsečík s osou x funkce f: y = 3x je roven: . Průsečík s osou y funkce f: y = 6x + 16 je roven: .